Cansult's blog

即使愿望永远无法实现
我也不愿就这样放手

0%

比赛总结 TJU [2020夏季训练] 组队赛6

Posted on Edited on In

懂了 不组队就不会坑队友了

C. Function

我觉得我会

但是我不会

我开始想的算每个数a[i]在n == x时会被加多少次c[x][i], 然后发现c[x][i] = c[x - 1][i] + c[x - 1][i - 1] + 1, 然后就不会求了

首先: 你要知道\(f(l, r)\)会在答案里出现\(\binom{l - 1+ n -r}{l - 1}\)次: 可以看作不断把\(f(l, r)\)变为\(f(l - 1, r)\), 或者\(f(l, r + 1)\).

然后: 你需要知道对于每个数a[i], 只需要找到所有包含位置\(i\)的\(f(l, r)\)出现的次数, 然后加和就可以了

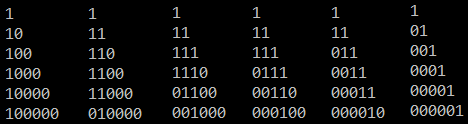
然后你发现对于a[1]到a[n], 他需要加起来的那些组合数在帕斯卡三角中的位置是这样的:

然后发现a[1]到a[i + 1]是加上了一列组合数, 然后删掉了一条斜线上的组合数

然后用两个公式就可以\(\mathrm O(n)\)递推了 \[ \sum _{i=0} ^{n} \binom {i} {k} = \binom {n+1}{k+1}\\ \sum _{i=0} ^{n} \binom {m+i} {i} = \binom {n+m+1}{n} \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define f(i, x, n) for(int i = x; i < (int)(n); ++i)

int const N = 1000000, md = 1e9 + 7;
int fc[N + 1], inv[N + 1], fcin[N + 1];

void ad(int &x, int y) { if ((x += y) >= md)x -= md; }
void sb(int &x, int y) { if ((x -= y) < 0)x += md; }
int ch(int n, int r) { return (ll)fc[n] * fcin[r] % md * fcin[n - r] % md; }

void solve(){
    int n;
    scanf("%d", &n);
    int s = 0, an = 0;
    f(i, 0, n){
        ad(s, ch(n, i + 1));
        int t;
        scanf("%d", &t);
        ad(an, (ll)t * s % md);
        sb(s, ch(n, i));
    }
    printf("%d\n", an);
}

int main(){
    fc[0] = 1;
    f(i, 1, N + 1)fc[i] = (ll)fc[i - 1] * i % md;
    inv[1] = 1;
    f(i, 2, N + 1)inv[i] = md - md / i * (ll)inv[md % i] % md;
    fcin[0] = 1;
    f(i, 1, N + 1)fcin[i] = (ll)fcin[i - 1] * inv[i] % md;
    int t;
    scanf("%d", &t);
    while (t--)solve();
}

D. Two Sequences

水题

不开O2甚至会T

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#pragma GCC optimize(2)

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <set>
#define MAXN (100000)
using namespace std;
set<int> a, b;
inline int getint() {
	int re = 0;
	char x = 0;
	while (x < '0' || x > '9') x = getchar();
	while (x <= '9' && x >= '0') re = (re << 1) + (re << 3) + x - '0', x = getchar();
	return re;
}
int main() {
	int t = getint();
	while (t--) {
		a.clear(), b.clear();
		int n, k;
		n = getint(), k = getint();
		for (int i = 1; i <= n; i++) a.insert(getint());
		for (int i = 1; i <= n; i++) b.insert(getint());
		set<int>::iterator x = a.end();
		for (set<int>::iterator i = a.begin(); i != a.end(); ++i) {
			set<int>::iterator bx = b.lower_bound(*i);
			if (bx == b.end() || *bx != *i) x = i;
			else b.erase(bx);
		}
		if (b.size() > 1 || (!b.empty() && abs(*b.begin() - *x) > k)) puts("NO");
		else puts("YES");
	}
	return 0;
}

H. Win Strategy

写了个贪心, 让最后一道题结束的时间尽量靠前

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
// 贪心 在当前时间i下, 把剩下的题分为两组, 一组是a在i前(按b排), 一组是a在i后(按(a + b)排), 比较两组的队首, 然后取一个数 

// #pragma GCC optimize(2)

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <set>
#define MAXN (1000)
using namespace std;
struct tas {
	int a, b, bh;
	bool operator == (const tas& x) {
		return (x.a == a && x.b == b);
	}
} ab[MAXN + 5];
struct cmp1 {
	bool operator () (tas x, tas y) { return x.b < y.b; }
};
struct cmp2 {
	bool operator () (tas x, tas y) { return x.a + x.b < y.a + y.b; }
};
int n, l;
bool vis[MAXN + 5];
int main() {
	int t;
	scanf("%d", &t);
	while (t--) {
		memset(vis, false, sizeof(vis));
		scanf("%d%d", &n, &l);
		for (int i = 1; i <= n; i++) scanf("%d%d", &ab[i].a, &ab[i].b), ab[i].bh = i;
		int ans = 0, j = 1;
		multiset<tas, cmp1> alr;
		multiset<tas, cmp2> fut;
		for (int i = 1; i <= n; i++) fut.insert(ab[i]);
		for (int i = 1; i <= l;) {
			for (; j <= n && ab[j].a <= i; j++)
				if (!vis[j]) {
					multiset<tas>::iterator x = fut.lower_bound(ab[j]);
					if (x != fut.end())
						fut.erase(x), alr.insert(ab[j]);
				}
			if (!alr.empty() && (fut.empty() || (alr.begin()->b + i < fut.begin()->a + fut.begin()->b))) {
				if (alr.begin()->b + i <= l) {
					i = alr.begin()->b + i;
					vis[alr.begin()->bh] = true;
					alr.erase(alr.begin());
					++ans;
				}
				else break;
			}
			else {
				if (!fut.empty() && (fut.begin()->a + fut.begin()->b <= l)) {
					i = fut.begin()->b + fut.begin()->a;
					vis[fut.begin()->bh] = true;
					fut.erase(fut.begin());
					++ans;
				}
				else break;
			}
		}
		printf("%d\n", ans);
	}
	return 0;
}

蛋是WA了

看题解直接背包 \(\mathrm O(2.5 \times 10^8)\), 不愧是你

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <bits/stdc++.h>
using namespace std;

typedef pair<int,int> pii;
const int N = 1001;
int n , l , dp[N][N],T;

pii a[N];

int calc(int idx , int time){
    if(idx > n || time > l+1)return -N;
    if(idx == n && time == l+1)return 0;
    int &ret = dp[idx][time];
    if(ret != -1)return ret;
    ret = max(calc(idx,time+1),calc(idx+1,time));
    if(time >= a[idx].first)
        ret = max(ret,1+calc(idx+1,time+a[idx].second));
    return ret;
}
int main(){
    cin >> T;
    while(T--){
        memset(dp,-1,sizeof dp);
        cin >> n >> l;
        for (int i = 0; i < n; ++i)scanf("%d%d",&a[i].first,&a[i].second);
        printf("%d\n",calc(0,1));
    }

    return 0;
}

By Cansult