Cansult's blog

即使愿望永远无法实现
我也不愿就这样放手

0%

学习笔记 KMP

Posted on Edited on In

今天正好xMinh问我KMP的实现来着...于是我就带着下面这首带劲的bgm给他讲了一下下...正好当补个档吧

做了一点微小的贡献 bgm请点开全文

↑彻底确定了我 slyz逗逼担当的地位

kmp靠的就是

智慧~ 大智慧~ 不一样的智慧~

我的烤馍片

请试想我以上图的姿态给xMinh讲KMP对其造成的心理阴影面积

沙茶的 KMP不详解(代码)

KMP可以以\(\mathrm O(n + m)\)的复杂度解决字符串的匹配问题

在普通的字符串匹配中, \(B\)串一旦在某一位(比如说第\(i\)位)上与\(A\)不一样, 就需要从头开始匹配\(B\)串, 这样最坏的复杂度是\(\mathrm O(m n)\)的

优化的一般思想都是利用重复的信息, 我们发现, 既然\(B\)在第\(i\)位与\(A\)失配了, 那么其实\(B\)的前\(i - 1\)位都是和\(A\)匹配的, 我们可以利用这个来优化

直接讲代码吧...xMinh说主要就是代码不懂...

代码是去年写的...那时候还似懂非懂来着...然后码风也比较...清新...

预处理

\(p[i]\)的意义: 在\(B\)的前\(i\)位, 最长的[前缀与后缀相等的长度], 也就是\((b[0] \to b[p[i]]) = (b[i - p[i]] \to b[i - 1])\) (不要在意边界...大体意思懂了就好... = =+)

1
2
3
4
5
6
7
8
9
10
n=strlen(a);
m=strlen(b);
p[0]=p[1]=0;
int j=0; // p[i]: (b[0] ~ b[p[i]]) = (b[i - p[i]] ~ b[i - 1])
for(int i=1;i<m;i++)
{
	j=p[i]; // 
	while(j&&b[j]!=b[i])	j=p[j];
	p[i+1]=(b[i]==b[j])?(j+1):0;
}

这个是什么意思呢...我们在预处理\(p[]\)...但是怎么预处理呢...肯定不能直接暴力匹配...那就\(n^2\)了是不...

\(j = p[i]\)
预处理

上图中, 蓝色的部分是已经确定的 前缀 == 后缀 长度, 当前匹配的是绿色的部分, 后半部分的绿色点是\(i++\)后得到的 , 前面的绿色点是\(j = p[i]\)得到的

现在就是要匹配第\(i\)位和第\(j\)位, 如果能匹配成功当然好, 直接把\(p[i + 1] = p[i] + 1\)即可

\(while (j \&\& b[j] != b[i]) \,\, j = p[j]\)
失配: 预处理

如果匹配失败, 我们发现既然我们已经知道前\(j\)位的\(p\), 也就是紫色的1部分和2部分相等, 而两个蓝色的部分是相等的, 所以2和3是相等的, 也就是 \[ \begin{cases} 1 = 2 \\ 2 = 3 \\ \end{cases} \to \,\, 1 = 3 \] 所以我们惊喜的发现, 1和3其实是相等的, 没有必要再去匹配了...我们可以直接匹配第\(j\)位和第\(i\)位, 如果不匹配, 可以继续类似递归一样继续下去...

1
2
3
4
5
6
7
8
9
10
n=strlen(a);
m=strlen(b);
p[0]=p[1]=0;
int j=0; // p[i]: (b[0] ~ b[p[i]]) = (b[i - p[i]] ~ b[i - 1])
for(int i=1;i<m;i++)
{
	j=p[i]; // j是当前应该和i(也就是当前长度字符串结尾)匹配的位
	while(j&&b[j]!=b[i])	j=p[j]; // 类似递归的处理过程, 知道递归到最底层无法递归: j回到开头了
	p[i+1]=(b[i]==b[j])?(j+1):0;
}

↑再粘一遍加深一下印象

匹配

终于到了激动人心的匹配...

1
2
3
4
5
6
7
8
9
10
11
j=0;
for(int i=0;i<n;i++)
{
	while(j&&a[i]!=b[j])	j=p[j];
	if(b[j]==a[i])	j++;
	if(j==m)
	{
		printf("%d\n",i-m+2);
		j=p[j];
	}
}
\(while (j \&\&a[i] != b[j])\,\, j = p[j]\)
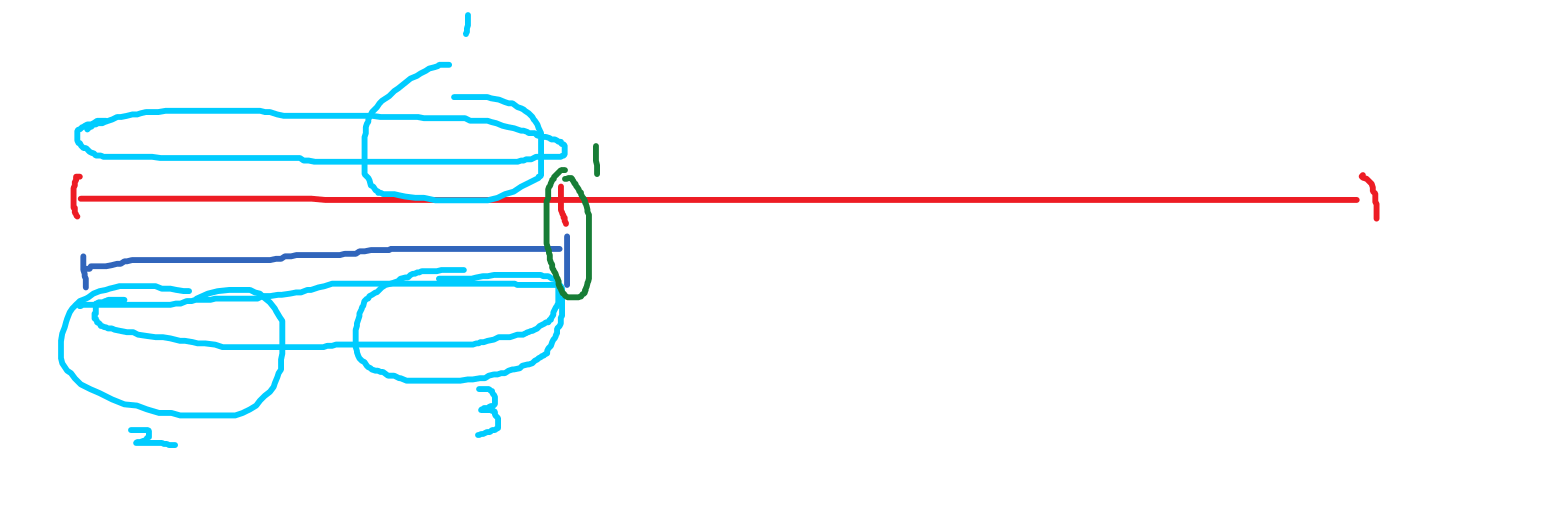
失配: 匹配中

当前在匹配绿色的1, 然后如果失配了...

我们发现 \[ \begin{cases} 1 = 3 \\ 2 = 3 \end{cases} \to \,\, 1 = 2 \] 于是我们又省了一堆匹配...直接从2的结尾开始匹配绿色的1就好了

\(j=p[j]\)

不得不说...xMinh跟我说不理解这个地方的时候还是挺吃惊的...这个的意思呢, 就是你kmp匹配, 不能光找出第一个匹配的串啊, 还得找出来后面那些是匹配的啊

其实这里就是把他当失配, 来尽快的找后一个可以匹配的串

也就是相当于两个串变成了下面这样:

失配: 假的

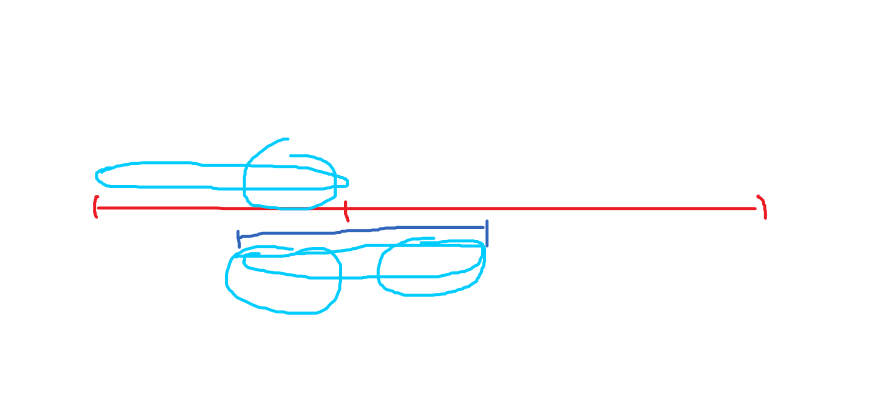
懂了?

例题

简单水题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
#define MAXN 1000000+5
#define MAXM 1000+5
using namespace std;
char a[MAXN],b[MAXM];
int n,m;
int p[MAXM];
int main()
{
	scanf("%s",a);
	scanf("%s",b);
	n=strlen(a);
	m=strlen(b);
	p[0]=p[1]=0;
	int j=0; // p[i]: (b[0] ~ b[p[i]]) = (b[i - p[i]] ~ b[i - 1])
	for(int i=1;i<m;i++)
	{
		j=p[i]; // 
		while(j&&b[j]!=b[i])	j=p[j];
		p[i+1]=(b[i]==b[j])?(j+1):0;
	}
	/*for(int i=0;i<m;i++)
	{
		cout<<p[i]<<" ";
	}
	cout<<endl;*/
	j=0;
	for(int i=0;i<n;i++)
	{
		while(j&&a[i]!=b[j])	j=p[j];
		if(b[j]==a[i])	j++;
		if(j==m)
		{
			printf("%d\n",i-m+2);
			j=p[j];
		}
	}
	for(int i=1;i<=m;i++)
	{
		printf("%d ",p[i]);
	}
	return 0;
}

脑洞进阶

见我的blog吧...

反正我当时没有想出来[苦笑]...

By 沙茶 Cansult