神仙做法
懵逼的 题目
Orz
扯淡的 题解
dls出的题果然思路清奇啊/cy
首先我们发现这个题啊 他这个头尾的限制肥肠不得劲,
如果我们在前后都加一个\(0\)的话,
我们会发现变化的规则都一样了
现在我们让变化规则统一变成了\(a_{i, j} =
a_{i - 1, j - 1} \oplus a_{i- 1, j + 1}\)
强迫症舒服了.jpg
然后我们又发现, 如果我们把这个序列(不包括头尾的两个\(0\))倒着复制一遍, 粘到末尾\(0\)的后面, 也就是
\[
a_0 = 0, a_1, a_2, \cdots, a_n, a_{n + 1} = 0, a_{n + 2} = a_{n}, a_{n +
3} = a_{n - 1}, \cdots, a_{2n + 1} = a_1
\]
然后首尾相接变成一个环
这样有什么用呢 因为对于对于我们加进去的两个\(0\)来说这个环是对称的, 也就是说\(0\)两边的数都是一样的,
所以我们加进去的\(0\)在不管进化多少次之后都会是\(0\)
这样我们可以保证这个对称的两边不会互相影响(不会跨过这个分界)
既然这样我们对这个环操作完了之后 原序列在环上位置的那些数就是答案
那么我们现在只需要考虑:
在一个环上我们怎么计算[每一个点都变成他两边点的异或值]这样\(T\)次后这个环的样子
然后我们发现 在这个每一次操作每个点都变成两边点异或值的序列中
当操作数为\(2^d\)时,
a[i][j] = a[i - 2^d][j - 2^d] xor a[i - 2^d][j + 2^d]
这是为是什么呢... 我们先打一个小表...
1
2
3
4
5
6
7
| a[i][j]
= a[i - 1][j - 1] xor a[i - 1][j + 1]
= a[i - 2][j - 2] xor a[i - 2][j] xor a[i - 2][j] xor a[i - 2][j + 2]
= a[i - 3][j - 3] xor a[i - 3][j - 1] xor a[i - 3][j + 1] xor a[i - 3][j + 3]
= a[i - 4][j - 4] xor a[i - 4][j - 2] xor a[i - 4][j - 2] xor a[i - 4][j] xor a[i - 4][j] xor a[i - 3][j + 2] xor a[i - 4][j + 2] xor a[i - 4][j + 4]
= a[i - 5][j - 5] xor a[i - 5][j - 3] xor a[i - 5][j + 3] xor a[i - 5][j + 5]
= a[i - 6][j - 6] xor a[i - 6][j - 4] xor a[i]
|
然后稍微画一下 其实是这个样子的
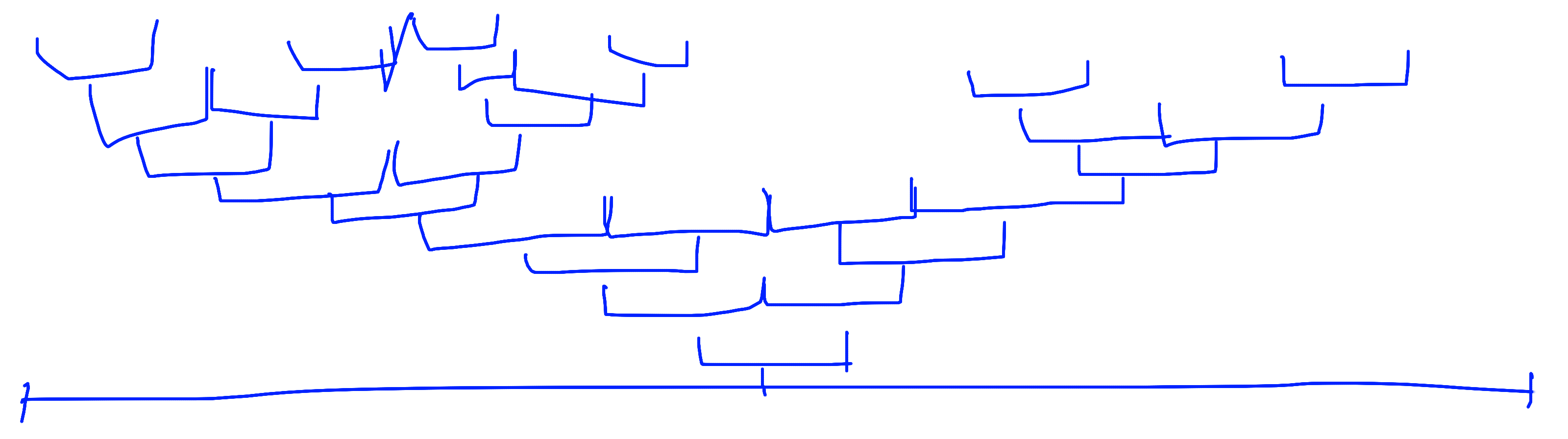
我们仔细观察然后就能发现这个玩意每消掉一次之后就会需要同样的时间来消掉下一次...嗯...意会一下吧_(:з」∠)_
知道这玩意了以后就可以对\(T\)二进制拆分了...注意是拆分不是分解...Emmmm...大体意思就是下一个1出现的时候基础是上一个1修改后的数组...
dls出的题果然思路清奇啊/cy
沙茶的 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| #include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#define MAXN (100000 + 5)
#define LL long long
using namespace std;
int n, a[MAXN << 1], ans[MAXN << 1];
LL t;
int cal(LL x)
{ return ((x) % (n + 1) + n + 1) % (n + 1); }
int main()
{
scanf("%lld%d", &t, &n);
for (int i = 1; i <= n; i++)
scanf("%1d", &a[i]);
for (int i = 1; i <= n; i++)
a[n + 1 + i] = a[n - i + 1];
n = (n << 1) | 1;
for (int i = 0; i < 63; i++)
if (t & (1ll << i))
{
for (int j = 0; j <= n; j++)
ans[j] = a[cal(j - (1ll << i))] ^ a[cal(j + (1ll << i))];
for (int j = 0; j <= n; j++)
a[j] = ans[j];
}
for (int i = 1; i <= (n >> 1); i++)
printf("%d", ans[i]);
return 0;
}
|
By 联赛钦定爆零的 Cansult
